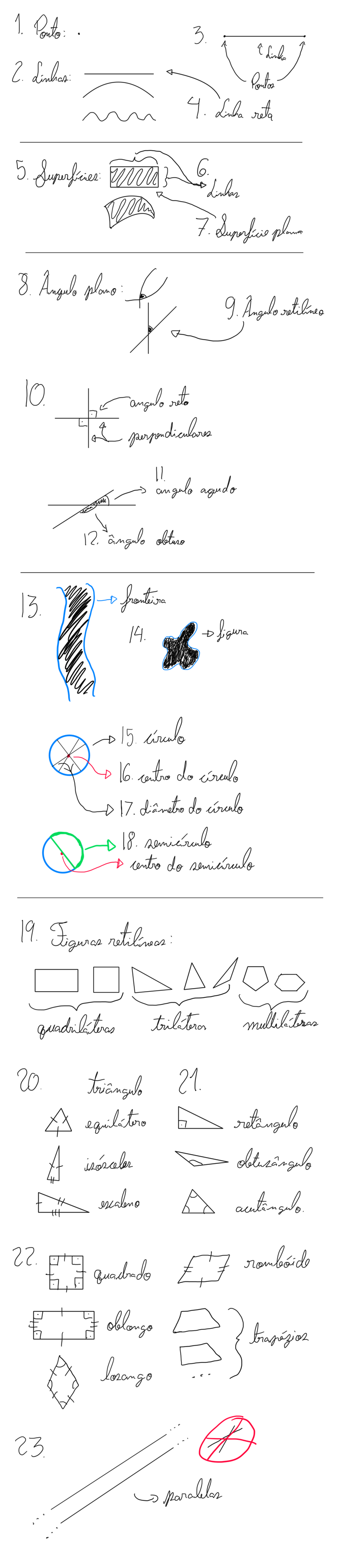
Definições
-
Um ponto é o que não tem partes.
-
Uma linha é comprimento sem largura.
-
As extremidades da linha são pontos.
-
Uma linha reta é a que está posta por igual com os pontos sobre si mesma.
-
Uma superfície é o que tem comprimento e largura.
-
As extremidades da superfície são linhas.
-
Uma superfície plana é a que está posta por igual com as retas sobre si mesma.
-
Um ângulo plano é a inclinação recíproca de duas linhas, que se tocam em uma superfície plana, e não estão postas sobre uma reta.
-
E quando as linhas que contêm o ângulo são retas, o ângulo é chamado retilíneo.
-
Quando uma linha reta, caindo sobre outra linha reta, fizer com esta dois ângulos iguais, um de uma, e outro de outra parte, cada um destes ângulos iguais se chama ângulo reto; e a linha incidente se diz perpendicular à outra linha sobre a qual cai.
-
Um ângulo obtuso é o que é maior que o ângulo reto.
-
Um ângulo agudo é o que é menor que o ângulo reto.
-
Uma fronteira se diz daquilo que é extremidade de alguma coisa.
-
Uma figura é um espaço fechado por uma ou mais fronteiras.
-
Um círculo é uma figura plana fechada por uma só linha, de maneira que todas as linhas retas, que de um certo ponto existente no meio da figura se conduzem para a linha referida, são iguais entre si.
-
O ponto referido se chama centro do círculo.
-
Um diâmetro do círculo é qualquer linha reta que passa pelo centro e que se termina por ambas as partes na circunferência. Tal linha também bissecciona o círculo.
-
Um semicírculo é uma figura compreendida entre o diâmetro e aquela parte da circunferência do círculo que é cortada pelo diâmetro. E o centro do semicírculo é o mesmo que o do círculo.
-
Figuras retilíneas são as que são formadas por linhas retas. Figuras triláteras são aquelas que são formadas por três linhas retas, quadriláteras são aquelas que são feitas por quatro linhas retas, e multiláteras são as que são feitas por mais de quatro linhas retas.
-
Entre as figuras triláteras, um triângulo equilátero é o que tem os três lados iguais, um triângulo isósceles é o que tem apenas dois lados iguais, e um triângulo escaleno é o que tem os três lados desiguais.
-
Além disso, entre as figuras triláteras, um triângulo retângulo é o que tem um ângulo reto, um triângulo obtusângulo é o que tem um ângulo obtuso, e um triângulo acutângulo é o que tem todos os ângulos agudos.
-
Entre as figuras quadriláteras, um quadrado é o que é juntamente equilátero e retângulo; um oblongo é o que é retângulo mas não equilátero; um losango é uma figura equilátera, mas não retângula; um rombóide é uma figura que, tendo os lados postos iguais, nem é equilátera, nem equiângula. Todas as demais figuras quadriláteras, que não são as referidas, chamam-se trapézios.
-
Linhas paralelas são linhas retas que, existindo no mesmo plano, e sendo prolongadas ilimitadamente em cada um dos lados, nunca chegam a tocar-se em nenhum deles.
POSTULADOS
Que fique postulado o seguinte:
- Traçar uma reta a partir de qualquer ponto até qualquer ponto.
- Prolongar uma reta finita, continuamente, sobre uma reta.
- Descrever um círculo com qualquer centro e distância.
- Que todos os ângulos retos são iguais entre si.
- Que caso uma reta, caindo sobre duas retas, faça os ângulos interiores e do mesmo lado menores do que dois ângulos retos, as duas retas, sendo prolongadas ilimitadamente, tocam-se no lado no qual estão os ângulos menores do que dois ângulos retos.
NOÇÕES COMUNS
- Coisas que são iguais à mesma coisa são iguais entre si.
- Se iguais forem adicionados a iguais, os todos são iguais.
- Se iguais forem subtraídos de iguais, os restos são iguais.
- Coisas que coincidem uma com a outra são iguais entre si.
- O todo é maior do que a parte.
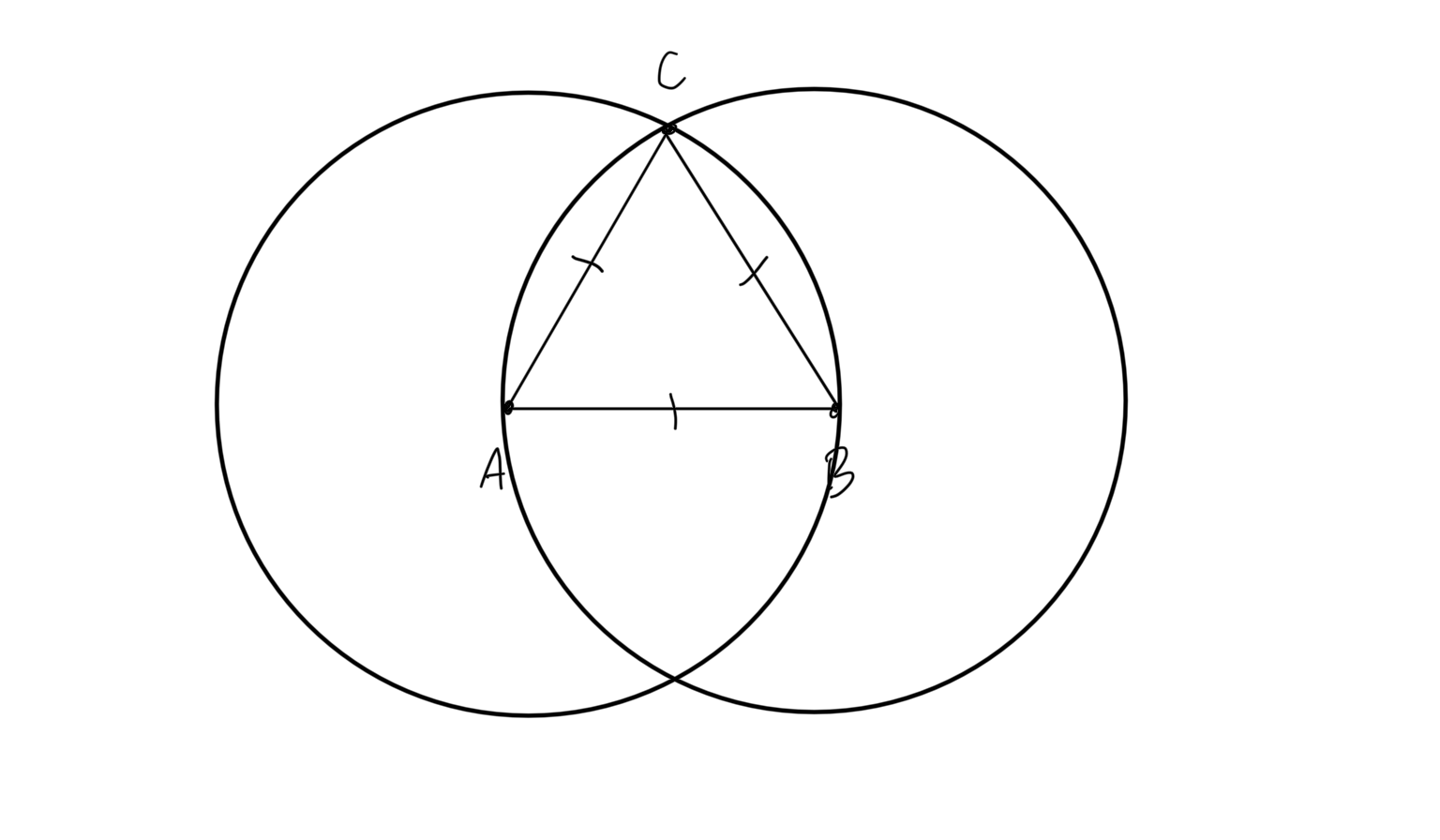
PROPOSIÇÃO I.1
Sobre uma linha reta determinada descrever um triângulo equilátero.
- Seja a linha reta AB de um certo comprimento finito.
- Deve-se sobre ela descrever um triângulo equilátero.
- Com o centro A, e com a distância AB se descreva (Postul. 3) o círculo BCD
- Com o centro B, e com a distância BA se descreva o círculo ACE (Postul. 3). - Do ponto C, onde os círculos se cortam reciprocamente, sejam traçadas (Post. 1.) para os pontos A, B as retas CA, CB.
- Sendo o ponto A o centro do círculo BCD,
- será AC = AB (Def. 15). - E sendo o ponto B o centro do círculo CAE,
- será BC = BA.
- Mas foi também provado que CA = AB.
- Logo, tanto CA, como CB, são iguais a AB.
- E coisas que são iguais a uma terceira, são iguais entre si (Noção comum 1).
- Logo será CA = CB.
- Logo as três retas CA, AB, BC são iguais.
- Por conseqüência, o triângulo ABC, feito sobre a reta dada AB, é equilátero; o que era preciso fazer.
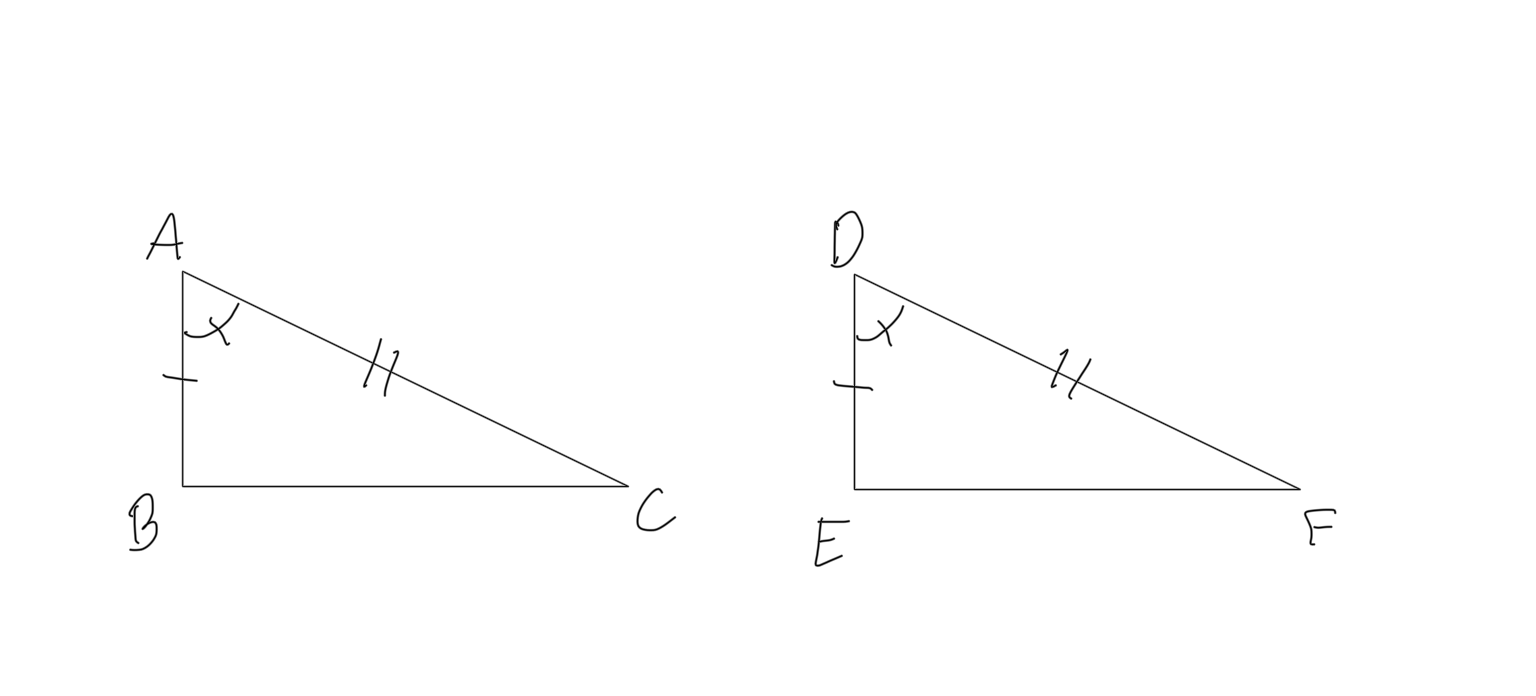
PROPOSIÇÃO I.4
Se dois triângulos tiverem dois lados iguais a dois lados, respectivamente, e os ângulos, compreendidos por estes lados, forem também iguais; então as bases e os triângulos, e os demais ângulos, que são opostos a lados iguais, serão também iguais.
- Sejam dois triângulos ABC, DEF, cujos lados AB, AC, DE, DF são respectivamente iguais, isto é, AB = DE, e AC = DF; e seja o ângulo BAC = EDF.
- Digo que a base BC é igual à base EF; que o triângulo ABC é igual ao triângulo DEF; e que os outros ângulos do primeiro triângulo são respectivamente iguais aos outros do segundo, conform ficam opostos a lados iguais; isto é, o ângulo ABC = DEF, e o ângulo ACB = DFE.
- Pois, se o triângulo ABC for posto sobre o triângulo DEF, de sorte que o ponto A caia sobre o ponto D, e a reta AB sobre a reta DE, então ponto B cairá sobre o ponto E, por ser AB = DE.
- Ajustando-se pois AB sobre DE, também a reta AC se ajustará sobre a reta DF, porque o ângulo BAC = EDF.
- Porque sendo AC = DF, o ponto C cairá sobre o ponto F.
- Mas temos visto que B cai sobre E.
- Logo, a base BC se ajustará sobre a base EF,
- e por conseqüência estas bases são iguais.
- Logo, a base BC se ajustará sobre a base EF,
- Logo todo o triângulo ABC se ajusta sobre todo o triângulo DEF, e assim são iguais.
- E os outros ângulos do primeiro triângulo também se ajustam sobre os outros do segundo e são iguais; isto é,
- o ângulo ABC = DEF,
- e o ângulo ACB = DFE; o que era preciso provar